Numerical optimisation and simulation for rational
metabolic engineering
Institute of Biological Sciences, Cledwyn Building,
University of Wales, Aberystwyth, SY23 3DD, United Kingdom
fax: + 44 1970 622354, phone: + 44 1970
622334, email: prm@aber.ac.uk,
| This is the electronic version of an article
published in the proceedings of the 8th BTK
meeting held in Göteborg in July 1998.
The full bibliographic reference to the hard-copy version of this article
is: |
| Mendes, P. & Kell, D.B. (1998) Numerical
optimisation and simulation for rational metabolic engineering. in
BioThermoKinetics in the post genomic era (eds. C. Larsson, I.-L.
Påhlman and L. Gustaffson), Chalmers Reproservice, Göteborg, pp.
345-349. |
[ Introduction ] [
Model and Methods ] [ Results and
Discussion ] [ Acknowledgement ] [
References ]
Dating from the work of Chakrabarty [1], there is much
current interest in what has become known as Metabolic Engineering (e.g.
[2-5]), i.e. in increasing by a directed mechanism (usually by
rDNA technology, [6]) the concentrations or activities of
enzymes in a pathway of interest, with a view to increasing the flux towards
desirable products (or eliminating undesirable ones). However, if this is to be
done rationally, one must have a way of targeting those metabolic steps that
are to have the greatest effect on the fluxes of interest. Metabolic control
analysis (MCA) seems to be one good candidate for such a purpose [7-12]. Notwithstanding the power and utility of these approaches,
however, their take-up amongst biotechnologists has been less than widespread,
due arguably to three main factors: i) some of the mathematics
underpinning MCA is rather recondite from a biochemical point of view,
ii) MCA is exact only for small changes in parameters such as enzyme
concentrations (although in favourable cases its approximations for "large"
changes may be good, [13, 14]), and
iii) it is normally necessary to perform an extensive series of
experiments to find out the distribution of the control of flux in a metabolic
pathway between different enzymes before knowing which one(s) might be best to
clone (see e.g. [15-18]). Here we show that a practical way
of overcoming these limitations is to analyse the properties of an appropriate
model of the pathway of interest using computer simulation. We have developed
[19, 20] and are currently extending a
user-friendly metabolic simulator (Gepasi)
that is suitable for performing "what if?" experiments in numero prior
to undertaking a series of difficult and possibly misguided experiments. The
full specification of this software and related material is available over the
Internet at http://qbab.aber.ac.uk/softw/gepasi.html. There
are numerous uses for a friendly simulator of this type, including those in
education. Here we illustrate how numerical optimisation methods, recently
introduced in Gepasi, can be used as a tool for rational metabolic engineering
through the analysis of the steady-state behaviour of a hypothetical model of a
branched pathway.
We analyse the branched pathway depicted in Fig. 1.
Our interest is to find conditions for which the flux towards P1 is high. We
note that the structure of this pathway and the kinetics of its enzymes are
such that it is almost impossible to guess the behaviour of this system by
intuition. Apart from the conservation of the cofactor moiety
([A]+[AH]=constant), the first enzyme on the branch of interest is
substrate-inhibited and the AH form of the cofactor is a modifier of the first
enzyme of the other branch (following the Botts-Morales mechanism [21], AH can be either an activator or inhibitor depending on the
values of the kinetic constants).
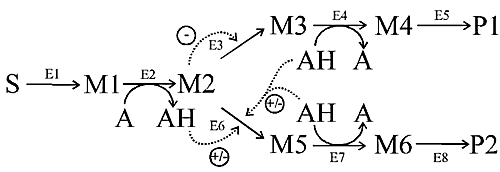
Figure 1 - Scheme of pathway analysed in the text.
Arrows represent the enzymatic steps and point to the forward direction of
flux, all reactions are chemically reversible. Dotted arrows represent
regulatory effects, the symbol +/- indicates that the effect can be either of
activation or inhibition. E1, E5 and E6 follow reversible Michaelian kinetics;
E2, E4 and E7 follow ordered Bi Bi kinetics in which the cofactor is always the
first to bind and the last to be released (this mechanism has 10 kinetic
parameters); E3 is inhibited by its own substrate (i.e. M2 binds both the
active and an inhibitory sites) and E6 follows the general Botts-Morales
modifier-type kinetics, in which the modifier can be an inhibitor or activator
depending on the values of the kinetic parameters (7 in total). We took the
reference state to have all kinetic constants, enzyme concentrations and total
concentration of the cofactor ([A]+[AH]) equal to 1. The equilibrium constants
of all steps are also 1, and are not changed in any simulation. All values are
in arbitrary units.
For this study we assume that we possess the technology to change
enzyme concentrations (by cloning) and to do site-directed mutagenesis on the
enzymes so that we could manipulate their kinetic parameters. The problem is
what parameters to manipulate to obtain i) high flux to P1 with low flux
to P2 and ii) high flux to P1 without affecting the flux to P2. In both
cases we limit the adjustable parameters by specifying upper and lower
boundaries, in addition ii) is also constrained by a fixed value of the
flux towards P2. We defined the pathway in Gepasi, attributed arbitrary
numerical values to the various parameters, simulated its steady state and took
this as the reference state (our wild type strain). Then we selected 35
parameters to be potential targets for manipulation: all the enzyme
concentrations, the total concentration of the cofactor plus 28 kinetic
parameters (all those for the ordered Bi Bi enzymes, and all those related to
the action of M2 as inhibitor of E3 and AH as modifier of E6. We allow these
parameters to be adjusted to values within 3 orders of magnitude on either side
of the "wild type" value.
In the most recent version of Gepasi we have devised an interface that
allows the program to combine numerical optimisation algorithms with steady
state or time course simulations. Apart from applications of the type described
here, this also allows the program to carry out robust parameter
estimation (fitting). This combination of optimisation and simulation has been
implemented in such a way that many different optimisation algorithms can be
used to attempt to solve a problem. This is an advantage as in numerical
optimisation there is no single algorithm that is best for all kinds of
problems [22]. The ability to apply several of these is then
almost a necessity for any moderately complex problem. In particular when the
number of adjustable parameters is large (e.g. more than 10) or when the
property to optimise is non-linear there is the high probability that there
will be many local optima. For the pathway of Fig. 1 we
have applied the following optimisation methods: random search, the Hooke and
Jeeves direct search [23], steepest descent, a limited memory
bounds-constrained quasi-Newton method (L-BFGS-B) [24], and a
genetic algorithm [25-27].
We want to maximise the steady-state flux of step 5 (J5) subject only to
bound constraints on the adjustable parameters. Using the new version of Gepasi
we applied 5 different optimisation algorithms to this problem. Analysis of the
results summarised in Table 1 reveals that the best
estimate for the maximum (J5=294.24) is 4 orders of magnitude higher than the
"wild type" and it was obtained with the direct search method of Hooke and
Jeeves. This is a local optimisation method that does not require information
from the gradient of the objective function; rather at each iteration it
generates a new search direction using a heuristic based on the results of a
few previous iterations. The second best solution was obtained with the genetic
algorithm, with a value of J5 only 2% lower than the best estimate. This method
required only 10% the number of simulations carried out by the Hooke and Jeeves
method. The two gradient descent methods (steepest descent and L-BFGS-B)
performed very badly (albeit still ten-fold higher than the "wild type").
Table 1 - Performance
of several optimisation methods for the maximisation of the flux to P1 (J5)
with simple bound constraints on the adjustable parameters. The wild
type entry refers to the initial state before applying the optimisation.
The last column lists the number of simulations that the optimisation method
required to reach the solution.
| Method |
J5 |
J8 |
[A]/[AH] |
Simulations |
| Wild type |
0.021139 |
0.033821 |
0.17651 |
1 |
| Steepest descent |
0.23389 |
0.060530 |
0.28111 |
308 |
| L-BFGS-B |
0.34677 |
0.31353 |
0.61628 |
1715 |
| Hooke & Jeeves |
294.24 |
1.3310 x10-5 |
0.60946 |
154195 |
| Genetic algorithm |
288.44 |
0.0050157 |
0.60550 |
10100 |
| Random search |
3.5908 |
0.012252 |
0.57515 |
10100 |
Comparing the parameter values of the "wild type" with our best
solution we conclude that the optimal value of J5 was obtained by setting the
concentration of all enzymes to their upper boundary value (1000) except E6
which was set to its lower boundary value (0.1). Interestingly this results in
the finding that the only enzyme of the branch to P2 to have control over J8 is
E6 (with a unity flux-control coefficient). However E1-E5 also control J8 but
their flux-control coefficients cancel each other. If one were to engineer this
pathway to increase the flux by 5 orders of magnitude for the same
concentration of substrate one would have to: i) over-express all
enzymes except E6 which must be under-expressed, ii) engineer all
enzymes such that they become as sensitive as possible to their substrates
and products (i.e. Km as low as possible), iii) engineer
the three Bi Bi enzymes such that their inhibition constants of the second
substrate and the first product are increased 1000-fold, but the one of the
first substrate only 100-fold iv) reduce the strength of inhibition of
E3 by its own substrate, v) increase the sensitivity of E6 towards its
modifier (AH) and in such a way that it becomes an inhibitor.
Table 2 - Performance
of several optimisation methods for the maximisation of the flux to P1 (J5)
subject to the constraint of flux towards P2 to be within 5% of the wild type
value.
| Method |
J5 |
J8 |
[A]/[AH] |
Simulations |
| Wild type |
0.021139 |
0.033821 |
0.17651 |
1 |
| Genetic algorithm |
23.385 |
0.033653 |
0.58172 |
100200 |
| Random search |
1.0846 |
0.033334 |
0.33144 |
100000 |
More interesting, from a biological point of view, is the case where
we want to maximise the flux towards P1 while keeping the competing flux to P2
essentially unchanged. In this case we have a constraint on one of the
variables of the model and unfortunately only a couple of the optimisation
methods can deal with this (random search and genetic algorithms). To implement
this constraint we have instructed Gepasi only to allow solutions for which
0.032<J8<0.034 (roughly the "wild type" value ± 5%). Our best
estimate for the maximum is 3 orders of magnitude higher (but this may actually
be far from the true maximum) which is a considerable improvement. The genetic
algorithm performed much better than the random search, as we anticipated.
Interestingly, for this constrained solution the concentration of both E6 and
E8 is reduced but not that of E7. The latter has a substrate and product common
to the flux being maximised.
Optimisation of biochemical models is inherently a hard process due to
the high dimensionality of the search space. If one were to examine the model
above with a brute-force method (that examines all combinations of n
values of each parameter) one would have to execute n35
simulations. It is obvious that such a solution is prohibitive, even on the
fastest computers and for small n. Additionally, in such a high
dimensional search space there are almost certainly numerous local optima, due
to the high non-linearity of some of the kinetic functions. Even if multiple
optima are not present, there will be large flat regions of parameter space
where methods based on gradients will halt. We have reasons to believe that
this is what happened with the gradient descent methods in our first example
(see Table 1).
We hope that the by making available our software, biochemists who do not necessarily
wish to develop this level of expertise in numerical analysis and computer
programming can still benefit from the use of simulation-optimisation
strategies.
We are indebted to the UK BBSRC for financial support.
[1] Chakrabarty, A.M. (1975)
United States patent no. 3,923,603
[2] Bailey, J.E.,
Birnbaum, S., Galazzo, J.L., Khosla, C. and Shanks, J.V. (1990) Ann. N. Y.
Acad. Sci. 589, 1-15.
[3] Bailey, J.E. (1991)
Science 252, 1668-1675. [abstract]
[4] Stephanopoulos, G. and Vallino, J.J. (1991)
Science 252, 1675-1681. [abstract]
[5] Cameron, D.C. and Tong, I. (1993) Appl. Biochem.
Biotechnol. 38, 105-140. [abstract]
[6] Skatrud, P.L., Tietz, A.J., Ingolia, T.D., Cantwell,
C.A., Fisher, D.L., Chapman, J.L. and Queener, S.W. (1989)
Bio/Technology 7, 477-485.
[7] Kell, D.B.
and Westerhoff, H.V. (1986) Trends Biotechnol. 4, 137-142.
[8] Kell, D.B. and Westerhoff, H.V. (1986) FEMS Microbiol.
Rev. 39, 305-320.
[9] Westerhoff, H.V. and
Kell, D.B. (1987) Biotech. Bioeng. 30, 101-107.
[10] Kell, D.B., van Dam, K. and Westerhoff, H.V. (1989) Symp.
Soc. Gen. Microbiol. 44, 61-93.
[11]
Cornish-Bowden, A., Hofmeyr, J.-H.S. and Cárdenas, M.L. (1995)
Bioorg. Chem. 23, 439-449.
[12] Westerhoff,
H.V. and Kell, D.B. (1996) J. Theoret. Biol. 182, 411-420. [abstract]
[13] Small, J.R. and Kacser, H. (1993) Eur. J.
Biochem. 213, 613-624. [abstract]
[14] Small, J.R. and Kacser, H. (1993) Eur. J.
Biochem. 213, 625-640. [abstract]
[15] Niederberger, P., Prasad, R., Miozzari, G. and
Kacser, H. (1992) Biochem. J. 287, 473-479. [abstract]
[16] Hofmeyr, J.H.S., Cornish-Bowden, A. and Rohwer, J.M.
(1993) Eur. J. Biochem. 212, 833-837. [abstract]
[17] Cornish-Bowden, A. and Hofmeyr, J.H.S. (1994)
Biochem. J. 298, 367-375. [abstract]
[18] Giersch, C. (1994) J. Theoret. Biol.
169, 89-99.
[19] Mendes, P. (1997) Trends Biochem.
Sci. 22, 361-363.
[20] Mendes, P. (1993)
Comput. Appl. Biosci. 9, 563-571. [abstract]
[21] Botts, J. and Morales, M. (1953) Trans. Farad.
Soc. 49, 696-707.
[22] Wolpert, D.H. and
Macready, W.G. (1997) IEEE Trans. Evol. Comput. 1, 67-82.
[23] Hooke, R. and Jeeves, T.A. (1961) J. Ass. Comput.
Mach. 8, 212-229.
[24] Byrd, R.H., Lu, P.,
Nocedal, J. and Zhu, C. (1995) SIAM J. Sci. Comput. 16,
1190-1208.
[25] Bäck, T., Fogel, D.B. and
Michalewicz, Z. (1997) Handbook of evolutionary computation,
IOPPublishing/Oxford University Press, Oxford. [synopsis]
[26] Michalewicz, Z. (1994) Genetic algorithms + data
structures = evolution programs, 3rd ed., Springer-Verlag, Berlin. [synopsis]
[27] Mitchell, M. (1995) An Introduction to Genetic
Algorithms, MIT Press, Boston. [information and
table of contents]
Copyright © 1998 Pedro Mendes &
Douglas B. Kell
 Home page
Home page

