An invited position paper for discussion among the participants of the NATO ARW on Technological and Medical Implications of Metabolic Control Analysis, Visegrad 10-16 April 1999
by
1Institute of Biological Sciences, Cledwyn
Building, University of Wales, Aberystwyth SY23 3DD, UK
2Present
address: National Center for Genome
Resources, 1800-A Old Pecos Trail, Santa Fe, New Mexico 87505, U.S.A.
*Corresponding author: phone +44 1970 622334 fax +44 1970 622354, email
dbk@aber.ac.uk
http://qbab.aber.ac.uk/home.htm
INDEX
[ Summary ] [ Introduction ] [ Assumptions in MCA ] [ All cells are not the same ]
[ Not all organisms are the same ]
[ Moiety conservation and flux enhancement ]
[ Modelling at the right scale ]
[ Critique of top-down methods ]
[ Proton-coupled electron transport-linked phosphorylation ]
[ Large changes and MCA ]
[ The not-very Universal Method ]
[ Multi-site modulation ] [ Active learning ] [ Acknowledgements ] [ References ]
We provide, as requested, a personal and critical survey of some of the major limitations of the principles and applications of metabolic control analysis, with special reference to the enhancement of fluxes of biotechnological interest.
Metabolic contol analysis and functional genomics share the same agenda, in that they seek to relate the presence and activities of individual genes and gene products to cellular biochemistry and physiology. They can be considered to differ, however, in a philosophical sense since the former is essentially deductive in character (and as practised) while the latter is of necessity inductive, at least initially, because so many ORFs are of unknown function. Inductive methods of machine learning should prove of value in unravelling their properties.
[ index ]
| "So the first requirement will be for a theoretical framework in which to embed all the detailed knowledge we have accumulated, to allow us to compute outcomes of the complex interactions and to start to understand the dynamics of the system. The second will be to make parallel measurements of the behaviour of many components during the execution by the cell of an integrated action in order to test whether the theory is right. Is there some other approach? If I knew it I would be doing it, and not writing about the problem." |
Sydney Brenner, 1997, in Loose Ends publ. Current Biology, London, p.73
Following its original formulation in 1973 (Heinrich & Rapoport, 1973; Heinrich & Rapoport, 1974; Kacser & Burns, 1973) as a means of understanding the contribution of the individual steps of a biochemical pathway to the values of flux and metabolite concentrations observed, some 13 years were to pass before we first surveyed (Kell & Westerhoff, 1986a; Kell & Westerhoff, 1986b) how the formalism, tools and terms of metabolic control analysis might usefully be applied to such systems in a biotechnological context. Since another such tridecennium has now elapsed, it is timely to take stock of progress, to recognise that the take-up of these methods among biotechnologists has been less than widespread, and (as requested by the Editor) to give a personal and critical review of successes, failures, problems and prospects for the use of MCA in biotechnology. In what follows, it is taken that the reader has a good working knowledge of the essential principles of MCA, as summarised for instance in (Cornish-Bowden & Cárdenas, 1990; Fell, 1992; Fell, 1996; Heinrich & Schuster, 1996; Kell et al., 1989; Kell & Westerhoff, 1986a; Ovádi, 1995) and on the Internet at http://dbk.ch.umist.ac.uk/mca_home.htm and in links therefrom. In addition, we shall concentrate on unicellular systems, implicitly those most commonly exploited to make products of biotechnological interest.
Perhaps the chief intellectual benefits of MCA have been the recognition (i) that in the steady state of a (linear) pathway where all steps are proceeding at the same rate it is nevertheless appropriate to recognise that each contributes quantitatively to the control of flux, in a manner which (for small or infinitesimal changes) can be summed to unity, (ii) that the flux-control coefficients so determined are consequently necessarily small, and (iii) that the activities of many steps must be changed simultaneously if fluxes are to be enhanced substantially. MCA thus constituted a bridge between the rather reductionistic view then prevalent (that we can understand a systems by looking at its component parts in isolation, without considering the interactions between them - see (Kell & Welch, 1991; Mendes et al., 1995)) and the holistic one (which in extremum - and in practice for many real, nonlinear, coherent, self-organising systems (Kell & Hitchens, 1983) - would hold that the whole is so much more than the sum of its parts that it is essentially pointless to consider the individual parts in isolation at all (Ho, 1998)).
Coupled to these aperçus has been the recognition that computer simulation can be a powerful tool in solving the forward problem of metabolism: given the parameters of the system (usually the external metabolite and effector concentrations and the kinetic properties of the enzymes) one can solve the relevant differential equations and predict the time course and - if such exist - the steady-state values of flux and metabolite concentrations. Software such as the program gepasi produced in aberystwyth by one of us (Mendes, 1993; Mendes, 1997; Mendes & Kell, 1998a, b) has been designed for (and indeed by) biologists (and successfully hides the mathematical details from the typical user), and given a simulation of a pathway it is easy to extract the ‘MCA properties’ such as flux- and concentration-control coefficients by numerical simulation of the effects of small changes in parameter values or analytically by differentiating the rate equations to acquire the elasticities and inverting the elasticity matrix so obtained (Fell, 1996; Fell & Sauro, 1985; Mendes, 1993; Reder, 1988; Westerhoff & Kell, 1987). The metabolic control anaysis of a system is thus normally ‘merely’ a snapshot of a typically rather restricted subset of the cellular biochemistry actually taking place in time and space.
[ index ]
With its concentration on small or infinitesimal changes, a domain where for (spatially) homogeneous systems its analysis is both exact and complete, MCA necessarily represents an approximation to a more complex reality, and this begs the question of how adequate this approximation is. In view of the recognition that it is but a subset of a full simulation of whatever system it is desired to simulate, it is probably unsupportable. Some other common assumptions of MCA (and its usual implementations) which will be explored later are summarised in Table 1. They include the implicit view that all cells in a suspension are the same, that it is possible to lump together large segments of metabolism without losing important knowledge of the behaviour of the overall system, and that there are ‘universal’ methods which can permit the rational optimisation of metabolic fluxes in systems of arbitrarily complex organisation.
Table 1. Some explicit and
implicit assumptions of modern MCA, and some inadequacies of its usual
implementations in a biotechnological context.
| Assumption / Misapplication | Comments / Consequences |
| All cells are the same | Heterogeneity is very much greater than normally assumed, and this can be determined experimentally using single-cell analyses |
| Simple models are adequate | Genome sequencing has uncovered the fact that we know the function of fewer than half of their genes, and there is evidence that almost all contribute to fitness even in laboratory conditions. Much more of metabolism is relevant to a flux than is normally recognised. |
| The Universal Method permits a rational approach to the optimisation of flux in any metabolic system | It doesn’t work if (i) the end-product feeds back to inhibit its own synthesis, whetehr kinetically or by mass action, and/or (ii) there are interactions between pathway branches involving moiety-conserved cycles. |
| The coefficients of MCA determined using large changes are not too badly different from those obtained via very small parameter changes | Nonlinearities, unknown interactions and the overall complexity of biological systems mean that deviation indices are reasonably small only in simple systems. |
[ index ]
Whilst it is rather obvious that the phenotypes of all cells in a differentiated organism are not the same (so much so that there is no such thing as a biochemically "normal" individual (Williams, 1956)), it is implicit in a standard MCA analysis that they are; in other words we tend to treat the system under study as an ensemble in the thermodynamic sense (Welch & Kell, 1986; Westerhoff & van Dam, 1987). In fact, the essence of the problem (Kell et al., 1991) is that one is trying, typically, to correlate a rate of change (v) of a certain variable with respect to the value of a certain parameter or property (p), but a correlation may be expected between the mean values and only if v is kinetically of first order with respect to p. This is completely unrealistic even for the axenic microbial cultures that are the focus of this review, and with the availability of techniques such as flow cytometry (Davey & Kell, 1996; Kell et al., 1991) it becomes possible to determine the heterogeneity of cellular properties directly. In one example of our own (Kaprelyants & Kell, 1992), the extent to which chemostat-grown (and thus as near as one can get to genuinely steady-state cultures of) Micrococcus luteus cells could take up the membrane energisation probe rhodamine 123 varied by more than 1000-fold under conditions in which uptake was fully uncoupler-sensitive and neither efflux pumps nor lack of membrane permeability were an issue. The unwanted consequence of the failure to take culture heterogeneity into account (in terms of being led to erroneous conclusions about causality and mechanism) reaches its apotheosis in the study of microbial viability/culturability (Kell et al., 1998). Such an analysis ignoring heterogeneity will also tend to mask intercellular interactions (Fuqua et al., 1996; Kell et al., 1995) such as those in which culturable cells secrete a factor necessary for the resuscitation and growth of non-growing cells of the same organism (Kaprelyants & Kell, 1993; Kaprelyants et al., 1994; Kaprelyants et al., 1999; Mukamolova et al., 1998).
[ index ]
So far as the typical textbook of biochemistry is concerned, cells are inevitably taken to be essentially similar, with a great majority of their broad activities (and the ‘housekeeping’ genes which code for them) being common throughout biology (at least at the level of prokaryote, eukaryote and archaean). Specific features such as photsynthesis or nitrogen fixation are seen merely as occasional adjuncts. Our attempts to simulate metabolism seem to rely implicitly on this, and it is perhaps assumed that models have a validity beyond the sytem for which they are constructed. However, as we enter the post-genomic era, two major facts have become evident; (i) many or most ORFs code for products of unknown function (Blattner et al., 1997; Bork et al., 1998; Cole et al., 1998; Goffeau et al., 1996; Hinton, 1997; Oliver, 1996) with many being conserved but most comparatively unique (Koonin & Galperin, 1997), and (ii) large-scale, genome-wide comparisons of orthologous genes point up the prevalence of horizontal gene transfer (Forterre, 1997a; Forterre, 1997b; Koonin et al., 1997; Rivera et al., 1998) and the consequent inadequacy of gradualist views of evolution. (Note however that these analyses are to date restricted to the very small fraction (Amann et al., 1995) of cultured microbes, and that many close relative of existing taxa remain to be cultured (Kaprelyants et al., 1999; Kell et al., 1998; McVeigh et al., 1996).) Consequently, we now recognise that many more genes contribute to fitness than had previously been considered.
The major approaches to functional genomics currently being undertaken involve the systematic knocking out of individual genes seriatim; where this is being done, e.g. in S. cerevisiae (Dujon, 1998; Oliver & Baganz, 1998; Oliver et al., 1998; Teusink et al., 1998), it is found that only some 15% are ‘essential’, and the question arises as to the role of the others - do they have a very high contribution to fitness under a restricted set of conditions met only occasionally and never in the laboratory, or do they all provide a marginal contribution to fitness? At least as judged by the fact that they are both transcribed under laboratory conditions in rich media and can be shown to contribute to fitness in sensitive growth rate tests (Eisen et al., 1998; Smith et al., 1995; Smith et al., 1996; Thatcher et al., 1998), one is led to attach significance to the latter view. The mental picture which emerges then is that whilst there may be core or major blocks of primary metabolism which are important, the contribution of the rest of the cellular activities which are normally neglected is likely to be just as great or greater. Although they may be individually small they are collectively numerous (the totals of genes in E. coli, baker’s yeast and Streptomyces coelicolor A3(2) are some 4000, 6000 and 8000 respectively), and while fewer will contribute to a flux than to the overall fitness as correctly judged (Kell, 1987; Westerhoff et al., 1983) by growth rate, the emerging paradigm is of a much greater complexity and sophistication of unicellular controls than we had heretofore recognised. One example of an important (and probably excessive) simplification in common usage is that the total values of pyridine nucleotides in cellular compartments are not of particular significance.
[ index ]
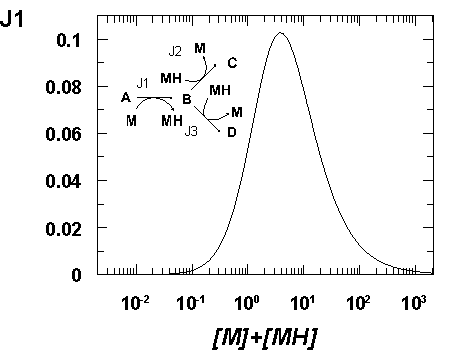
One aspect of metabolism that has received little attention for the purposes of flux maximisation is the existence of moiety-conserved cycles (Reich & Sel'kov, 1981). These are ubiquitous in metabolism and a few of them (e.g. NAD/NADH and ATP/ADP) act as major links between various parts of metabolism. Whilst affecting the poise of these cofactor couples can be most useful in metabolic engineering (Lopez de Felipe et al., 1998) the flux through a pathway, as seen within the MCA formalism (Hofmeyr et al., 1986), is also controlled by the total amount of conserved moieties. We have observed by computer simulation that the flux of several model pathways responds to the total amount of conserved moiety according to a bell-shaped curve. This suggests that there is an optimal amount of cofactor for a given pathway flux (and that compartmenation of pathways would be necessary to optimise them separately), otherwise the flux will be somewhat limited by the availability of the conserved moiety. To manipulate the total amount of the moiety we will thus need to target the pathways of their biosynthesis and degradation. Alternatively we could as well manipulate the number and/or affinity of moiety binding sites which modulate the amount of available (i.e. free) total moiety. The existence of large numbers of NAD binding sites may indeed be a cellular mechanism for the rapid adjustments of the available total amount of NAD (rather than a slower adjustment by increased/decreased biosynthesis). Fig. 1 depicts such a bell-shaped relation between the total amount of the moiety and the flux for a simple branched pathway in which other parameters are held constant.
 |
| Figure 1. Dependence of entry steady-state flux on the total amount of conserved moiety in a model branched pathway. The pathway simulated is shown in the inset, the arrows representing the positive direction of flux. All reactions are fully reversible, all kinetic and equilibrium constants are unity, [A] = 10, [C] = [D] = 1 such that the overall disequilibrium ratio is 0.1 on both branches. |
[ index ]
We have traditionally treated our systems relatively simply, due in part to the difficulty of measuring everything. With the emergence of measurements of the proteome (Anderson & Anderson, 1998; Wilkins et al., 1997), the transcriptome (de Saizieu et al., 1998; DeRisi et al., 1997; schena et al., 1996; Spellman et al., 1998; Velculescu et al., 1997; Wodicka et al., 1997) and the metabolome (Oliver & Baganz, 1998; Oliver et al., 1998) we now have the ability to carry out hundreds of measurements on macromolecular and metabolic variables simultaneously. The outcomes of the pioneering studies are in many cases given in the form of lists of expression ratios for the hundreds of genes of interest, which are hard to interpret - the appropriate scale for easy understanding is not a life-sized model (Eisen et al., 1998). Treating related segments of metabolism as ‘blocks’ is one solution (Kell et al., 1989), sometimes referred to as top-down analysis (Brand, 1996; Brand, 1998; Brown et al., 1990) and is being exploited in functional genomics as the FANCY method (Oliver & Baganz, 1998; Teusink et al., 1998), but this approach fails to give a true account of the system of interest under a number of circumstances.
[ index ]
In the early literature of MCA (Kacser & Burns, 1973) it was already proposed that one could group sequential enzymes and treat them as one unit for the purposes of control analysis. This is possible due to the summation theorem (Kacser & Burns, 1973) and the fact that the elasticity concept can be applied to groups of reactions (Kacser, 1983). Brown et al. (Brown et al., 1990) took this one step further and formally proposed the ‘top-down’ method for determining control coefficients. In this method one builds two groups of metabolic steps around (upstream and downstream of) one single intermediate metabolite. Provided that this central intermediate metabolite is the only kinetic link between the two groups of steps then one can determine the elasticites of the two groups towards that metabolite with just two single-modulation experiments. Group control coefficients can then be calculated using the connectivity and summation theorems (the assumption therefore being that no other interactions - such as feedback loops or metabolic channelling (Agius & Sherratt, 1997; Mendes et al., 1995; Ovádi, 1995) - exist between the two groups). The control coefficients thus obtained for the two groups of steps could reveal which of them has more control, e.g. as in (Simpson et al. 1998; Stephanopoulos & Simpson, 1997), where knowledge of this can allow one to vary the control structure of a pathway to improve fluxes of biotechnological interest (Simpson et al., 1995).
An attractive application of this method would be to apply it repeatedly by subdividing each group into smaller groups. This would result in the determination of the complete control structure of the pathway, each time with more resolution (hence the ‘top-down’ name). Although elegant in conception, this method is effectively impossible in practice, due to the requirement of grouping steps such that there is only one kinetic link (via the intermediate metabolite) between them. Ainscow and Brand have recently extended the method (Ainscow & Brand, 1995) such that it can be applied to the case when the groups of steps are connected by more than one metabolite. Nevertheless, for the method to work as intended one must be absolutely sure that all the kinetic links between the groups of steps are known and included in the analysis explicitly (or are unaffected by the modulations performed (Ainscow & Brand, 1998a)). Thus, one can never be sure that the coefficients determined by this method are correct as there could be extra kinetic interactions between the two groups of steps other than the ones taken into consideration. The classical method of direct determination of control coefficients by perturbation of enzyme activities is immune from this problem and so could (and should) be used to confirm the results with the top-down method - but this rather defeats the purpose of using it in the first place! (Recently, Kholodenko and colleagues have presented a combination of top-down MCA and the perturbation method which they refer to as ‘Metabolic Design Analysis’ (Kholodenko et al., 1998).) But there are extra problems when one wants to use this method in general: (i) there are several known (and certainly many more unknown) feedback loops in metabolism and (ii) many reactions include cosubstrates such as NAD/NADH or ATP/ADP which form kinetic links between steps normally considered distant. Both these reduce the number of metabolites that can be effectively used in the top-down approach to separate groups of steps. As such the method is not amenable, in general, to a true ‘top-down’ approach of measuring all control coefficients. The problems are greatly compounded by the propagation of errors and bias contingent on the measurement of elasticities (Schlosser et al., 1993; Thomas & Fell, 1995) and control coefficients (Ehlde & Zacchi, 1996; Small, 1993), and such errors may not be normally distributed (Ainscow & Brand, 1998b). We therefore find that the (correct) application of the top-down method to large, complex biosystems may be rather limited in practice, and above all dangerous if results are not validated by an independent method.
Note that this is not a critique of simplification per se, since in many cases the intrinsic dimensonality of the major blocks of a complex system of interest may well be comparatively small and the level of understanding that we require, and indeed good precision in our models (Broadhurst et al., 1997; Kell & Sonnleitner, 1995; Shaw et al., 1997), is more easily attained with small models than with large ones. But this is something that we find out afterwards, when measurements of many variables have been made and evaluated (Eisen et al., 1998), not something to build in beforehand!
[ index ]
A consequence of lumping reactions together in the macroscopic way typified by the top-down approach is that it is assumed that their intermediates are delocalised. One of the major areas of interest of this laboratory has been in the problem of channelling, most recently in terms of intermediary metabolites (Mendes et al.,1992 , 1995, 1996) but more classically in terms of the problem of whether the energetic intermediates of electron transport-linked phosphorylation are delocalised or not (Kell, 1979; Kell, 1988; Kell & Westerhoff, 1990). The basic idea is as follows. In the classical chemiosmotic coupling model (Mitchell, 1966; Nicholls & Ferguson, 1992), electron transport generates a transmembrane proton gradient which, due to the rapid diffusion rates of protons in aqueous media, leads to a delocalised protonmotive force Dp consisting of a membrane potential Dy and a pH gradient zDpH which is consequently avaiable to all ATP synthase enzymes in the organelle in whose membrane the pmf-generators are embedded. Uncouplers act by dissipating the pmf as heat. (In addition, the pmf can in principle feed back to inhibit electron transport via ‘slip’ or be dissipated ‘naturally’ to heat via a pmf-dependent ‘leak slip’ which does not differ formally from the imperfect coupling naturally present.) This is depicted in Fig 2.
 |
| Figure 2. The classical chemiosmotic coupling paradigm for electron transport-linked phosphorylation. |
The consequence is that the rate of phosphylation Jp depends only and monotonically on Dp, typically according (when assessed experimentally by acid-bath-type experiments) to a sigmoidal function of the pmf, i.e. :
| Jp = [ATP-synthase] . f(Dp) | (Eq. 1) |
In a typical dual-inhibitor titration using an uncoupler and an ATP synthase inhibitor, we first study the effect of uncoupler on Jp, with results similar to those in Fig 3 (open circles). We then inhibit half of the ATP synthases using a tight-binding (or better covalent) inhibitor such that Jp falls to one half of its original value (Fig 3). The effect of the uncoupler titration that must be predicted from the delocalised chemiosmotic type of uncoupling model is similar to that given by the closed triangles in Fig 3, since the pmf canot be made smaller by this treatment and it is probably slightly larger due to the smaller drain on it - the shape of the curve is the same but the rate at any level of uncoupler (and putatively pmf) is just one half of the control. Similarly, the amount of uncoupler needed to achieve full uncoupling is the same. Unfortunately for this view, the experimental curve is quite different: lowering the initial Jp to one-half of its original value with the ATP synthase inhibitor decreases by one half the amunt of uncoupler necessary to achieve full uncoupling. No delocalised coupling model can account for this type of behaviour in uncoupler/energy transfer inhibitor titrations (Herweijer et al.,1986; Hitchens & Kell, 1983a; Hitchens & Kell, 1983b; Kell, 1988; Kell, 1992; Westerhoff & Kell, 1988), and indeed none has made a serious attempt to do so.
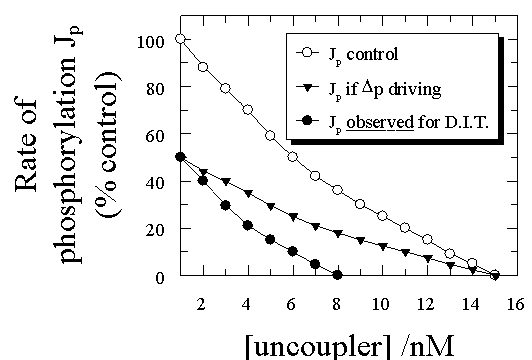 |
| Figure 3. Theoretical and experimental traces from dual uncoupler/energy transfer inhibitor titrations. |
[ index ]
As is well-known, and is mentioned above, the theorems of classical MCA work only for parameter changes which are small (and in principle infintesimal). However, it is to be assumed (and see below) that substantial increases in flux towards metabolites of biotechnological interest require large changes in at least some of the parameters such as enzyme concentrations (and the same is true for the phenotypic manifestation of disease states when a sufficient (‘theshold’) loss in enzymatic function is induced (Durrieu et al., 1997; Letellier et al., 1998; Mazat et al., 1997, 1998)). Small and Kacser tackled the problem of exactly how great an inaccuracy in estimating control coefficients via large changes in parameters might be involved. They first introduced the idea of a deviation index as the relative change in a metabolic variable such as a flux to a large change in a parameter (Small & Kacser, 1993a), and showed that for unbranched chains of enzymes with linear kinetics there was a direct relationship between deviation indices and flux-control coefficients. They also pointed out that combined changes of the activity of individual enzymes will produce a more-than-additive response (and see below). The behaviour of branched and non-linear pathways was more complex (Small & Kacser, 1993b), and though it was stated that many metabolic systems behave in practice as quasi-linear systems, the differences between the actual and predicted amplification factors were often quite great. Indeed, a detailed study by R. Schuster & Holzhütter (Schuster & Holzhutter, 1995) of erythrocyte properties resulting from large-scale alterations in enzymatic activities concluded that no existing extrapolation method using the conventional control coefficients was able to provide reliable predictions.
[ index ]
It is worth noting that, as proven in the summation theorem of Metabolic Control Analysis (e.g. Cornish-Bowden et al., 1995; Fell, 1996; Heinrich & Rapoport, 1974; Heinrich & Schuster, 1996; Kacser & Burns, 1973; Kell & Westerhoff, 1986a), changes in the concentrations of individual enzymes tend to have little effect on particular metabolic fluxes (nor, indeed, on the gross phenotype under most laboratory conditions (Thatcher et al., 1998)). However, in part because of the so-called connectivities of MCA, changes in individual enzyme concentrations can and do have substantial effects on metabolite concentrations, even when the changes in flux are negligible (Mendes et al., 1995; Mendes et al., 1996). It is therefore very reasonable that attempts to increase metabolic fluxes by increasing the concentrations of metabolic enzymes may lead to substantial increases in metabolite levels, and that these may either prove cytotoxic or at least necessarily lead to the diversion of flux to pathways other than that desired. It would therefore be desirable (if it were indeed possible) to seek to modulate fluxes by changing enzyme activities in a manner that managed to preserve the steady-state levels of metabolites. Thus Kacser and Acerenza (Kacser & Acerenza, 1993) introduced the so-called Universal Method that purported to have this effect and to be ‘entirely general’. In the Universal Method, it is recognised that in any pathway leading to the output of interest, the activities of whose enzymes one would wish to increase, there will be branch points leading to other parts of metabolism which should not be perturbed. Because of the conservation of mass, the fluxes down each branch point following a change in flux are related both to the changes in flux before and after the branchpoint in the ‘main’ pathway and to the ratio r of enzyme activities before and after the change in flux. For unimolecular reactions, there is a unique value of r for each such reaction at which the fluxes down the branches remain unchanged.
However, this method has two major failings: (i) it does not work when it is the end product itself which feeds back to inhibit its own production (and this is usually the case in any high-yielding fermentation, for both thermodynamic and kinetic reasons), and (ii) the method works in principle only for systems in which there are no interactions between pathways, such as those involving conserved moieties such as adenine and pyridine nucleotide couples. Since any system of interest is likely intimately to involve cofactors of this type, it seems that the Universal Method as presented is unlikely to prove of substantive utility, nor seems to have done so to date.
[ index ]
Whilst the Universal Method cannnot work as advertised, it does draw attention to the need - whatever the effects on the rest of metabolism - for multisite modulations to be performed if there is to be a substantial increase in flux, and this is now widely recognised (Cornish-Bowden, 1995; Cornish-Bowden et al., 1995; Fell, 1998; Fell & Thomas, 1995; Niederberger et al., 1992; Thomas & Fell, 1998). This does not contradict any of the insights of MCA, and in fact it can be shown both by analysis and simulation (Small & Kacser, 1993a, 1993b) that this result is to be expected: as soon as the step with higher control becomes faster (as happens with overexpression) the control shifts to other steps in the pathway. It is now evident that for any strategy to be successful in increasing the flux of a pathway substantially there is a requirement for the manipulation of several steps. This was clearly demonstrated experimentally by Niederberger and colleagues in their classical study (Niederberger et al., 1992) and has been discussed at some length by Fell and Thomas (Fell, 1998; Fell & Thomas, 1995; Thomas & Fell, 1998). In a recent conference it was evident that the metabolic engineering community (both research and industry) is converging to this conclusion, and it is now largely accepted that to increase flux one should manipulate at least two metabolic steps (Mendes & Kell, 1997). Removing the fluxes to unproductive pathways is likely to be much more significant for mature fermentations than seeking solely to stimulate the flux through the desired one per se (Holms, 1996; Holms et al., 1991).
[ index ]
The commonest conventional method of experimental science, generally referred to as ‘the scientific method’, involves the preparation of an experimental system in a specified state and the manipulation of, preferably, a single parameter, whereupon one observes the time-evolution of the values of one or more variables compared to that of a control in which the ‘triggering’ manipulation is not performed. The parameter may then be moved to different set points. Each of those variables might also be controlled at a fixed level, i.e. as a parameter, and comparable experiments performed. If the system is comparatively simple and well behaved (e.g. asymptotically stable, and not chaotic as in (Davey et al., 1996)) it is usually possible to determine the form and parameterisation of the equations relating the parameters and the variables and the time evolution of the system by mathematical fitting procedures (Mendes & Kell, 1998a), leading to what is usually considered an "understanding" of the system. However, this is true only for simple systems, and one may put forward the views that (i) this kind of deductive reasoning is that usually practised in the MCA community, (ii) the functional genomics agenda (Bork et al., 1998; Hieter & Boguski, 1997; Hinton, 1997; Kell, 1998; Oliver, 1996) is likely to be much better attacked under current conditions via an inductive type of approach.
Indeed, we consider that complex systems cannot be treated to best advantage (Westerhoff & Kell, 1996) in this more classical, deductive way. First of all, there are far too many variables and potential parameters for an exhaustive set of experiments to be performed, and those parameter sets producing ‘desirable’ outcomes may be few and far between. (For n parameters which might adopt m values the number of combinations is obviously mn, and even if m is only a miserable 2 for n=100, 2100 ~ 1031, and the lifetime of the Universe is ‘only’ some 1017s.) The inevitable conclusion for the study of complex systems is that we we must vary many (or at least several) parameters at a time and use the methods of multivariate statistics and machine learning to deconvolute the data so obtained to extract those features most relevant to the operation of the system. Then, because of the high dimensionality of the system and problem, we must iterate this process further (somewhat in the way in which we traditionally need to provide rounds of mutation and selection in fermentation development programmes (Crueger & Crueger, 1989)). Indeed, our own approach in recent years to the understanding of complex cellular systems has been to exploit spectroscopic methods such as pyrolysis mass spectrometry (Broadhurst et al., 1997; Gilbert et al., 1997; Goodacre & Kell, 1996; Goodacre et al., 1993, 1994a, 1994b, 1996a; Taylor et al., 1998), ft-ir (Goodacre et al., 1996b, 1998a; Oliver et al., 1998; Winson et al., 1997, 1998), and dispersive Raman (Goodacre et al., 1998b) in which hundreds of variables are measured simultaneously, and to couple these measurements with advanced chemometric and related analyses based on the methods of artificial intelligence, machine learning and evolutionary computing (Bäck et al., 1997; Michie et al., 1994; Rich & Knight, 1991; Weiss & Kulikowski, 1991).
Although the above described the overall structure of a single experiment, scientific research of course proceeds by a process of experimental hypothesis testing (e.g. Oldroyd, 1986), and it is appropriate to end by outlining one way of computer-assisted knowledge acquisition with which we think important progress might be made. This process is an active approach, which in fact differs markedly from the passive nature of most ‘scientific discovery’ systems (Langley et al., 1987), which either receive data all at once in a single batch, or have no choice over the next example (Raju & Cooney, 1998), and suffer from the problem that most of the observables have little bearing on the overall outcome (Blum & Langley, 1997) and for the purposes of this analysis amount to ‘noise’. The study of systems that can choose the next experiment is known as ‘active learning’. There are two computational tasks in active learning: formation of hypotheses that are consistent with known background knowledge and experimental results, and selection of the best experiment (or set of experiments) to discriminate between hypotheses. It should be noted that experiment selection in active learning is not to be confused with the traditional statistical study of experimental design, where the difference is between deciding which question to ask next (active learning) versus ensuring that a set of experiments can answer a question (traditional experimental design).
To conclude, it seems reasonable that active learning approaches can lead us efficiently to means for asking and answering the right kinds of question at the right kind of complexity in the post-genomic era.
[ index ]
We thank Ross King and Steve Oliver for useful discussions, and the BBSRC for financial support.
[ index ]
Agius, L. & Sherratt, H. S. A. (1997). Channelling in intermediary metabolism. Portland Press, London. [synopsis]
Ainscow, E. K. & Brand, M. D. (1995). Top-down control analysis of systems with more than one common intermediate. Eur. J. Biochem. 231, 579-586. [ abstract ]
Ainscow, E. K. & Brand, M. D. (1998a). Control analysis of systems with reaction blocks that 'cross-talk'. Biochim. Biophys. Acta 1366, 284-290. [ abstract ]
Ainscow, E. K. & Brand, M. D. (1998b). Errors associated with metabolic control analysis. Application of Monte Carlosimulation of experimental data. J. Theoret. Biol. 194, 223-233. [ abstract ]
Amann, R. I., Ludwig, W. & Schleifer, K. H. (1995). Phylogenetic identification and in situ detection of individual microbial cells without cultivation. Microbiol. Rev. 59, 143-169. [ abstract ]
Anderson, N. L. & Anderson, N. G. (1998). Proteome and proteomics: New technologies, new concepts, and new words. Electrophoresis 19, 1853-1861. [ abstract ]
Bäck, T., Fogel, D. B. & Michalewicz, Z. (1997). Handbook of evolutionary computation. IOPPublishing/Oxford University Press, Oxford. [synopsis]
Blattner, F. R., Plunkett, G., Bloch, C. A., Perna, N. T., Burland, V., Riley, M., ColladoVides, J., Glasner, J. D., Rode, C. K., Mayhew, G. F., Gregor, J., Davis, N. W., Kirkpatrick, H. A., Goeden, M. A., Rose, D. J., Mau, B. & Shao, Y. (1997). The complete genome sequence of Escherichia coli K-12. Science 277, 14531462. [ abstract ]
Blum, A. L. & Langley, P. (1997). Selection of relevant features and examples in machine learning. Artificial Intelligence 97, 245-271.
Bork, P., Dandekar, T., Diaz-Lazcoz, Y., Eisenhaber, F., Huynen, M. & Yuan, Y. P. (1998). Predicting function: From genes to genomes and back. J. Mol. Biol. 283, 707-725. [ abstract ]
Brand, M. D. (1996). Top down metabolic control analysis. J. Theoret. Biol. 182, 351-360. [ abstract ]
Brand, M. D. (1998). Top-down elasticity analysis and its application to energy metabolism in isolated mitochondria and intact cells. Mol. Cell. Biochem. 184, 13-20. [ abstract ]
Broadhurst, D., Goodacre, R., Jones, A., Rowland, J. J. & Kell, D. B. (1997). Genetic algorithms as a method for variable selection in multiple linear regression and partial least squares regression, with applications to pyrolysis mass spectrometry. Anal. Chim. Acta 348, 71-86.
Brown, G. C., Hafner, R. P. & Brand, M. D. (1990). A top-down approach to the determination of control coefficients in metabolic control theory. Eur. J. Biochem. 188, 321-325.
Cole, S. T., Brosch, R., Parkhill, J., Garnier, T., Churcher, C., Harris, D., Gordon, S. V., Eiglmeier, K., Gas, S., Barry, C. E., Tekaia, F., Badcock, K., Basham, D., Brown, D., Chillingworth, T., Connor, R., Davies, R., Devlin, K., Feltwell, T., Gentles, S., Hamlin, N., Holroyd, S., Hornby, T., Jagels, K., Krogh, A., McLean, J., Moule, S., Murphy, L., Oliver, K., Osborne, J., Quail, M. A., Rajandream, M. A., Rogers, J., Rutter, S., Seeger, K., Skelton, J., Squares, R., Squares, S., Sulston, J. E., Taylor, K., Whitehead, S. & Barrell, B. G. (1998). Deciphering the biology of Mycobacterium tuberculosis from the complete genome sequence. Nature 393, 537-544. [ abstract ]
Cornish-Bowden, A. (1995). Kinetics of multi-enzyme systems. In Biotechnology, vol. 9 (ed. H. J. Rehm, G. Reed, A. Pühler and P. Stadler), pp. 121-136. Verlag Chemie, Weinheim.
Cornish-Bowden, A. & Cárdenas, M. L. (1990). Control of metabolic processes. Plenum Press, New York. [ contents ]
Cornish-Bowden, A., Hofmeyr, J.-H. S. & Cárdenas, M. L. (1995). Strategies for manipulating metabolic fluxes in biotechnology. Bioorg. Chem. 23, 439-449. [ abstract ]
Crueger, W. & Crueger, A. (1989). Biotechnology: a textbook of industrial microbiology. Sinauer Associates, Sunderland, MA.
Davey, H. M., Davey, C. L., Woodward, A. M., Edmonds, A. N., Lee, A. W. & Kell, D. B. (1996). Oscillatory, stochastic and chaotic growth rate fluctuations in permittistatically-controlled yeast cultures. Biosystems 39, 43-61. [ abstract ]
Davey, H. M. & Kell, D. B. (1996). Flow cytometry and cell sorting of heterogeneous microbial populations: the importance of single-cell analysis. Microbiol. Rev. 60, 641-696. [ abstract ]
de Saizieu, A., Certa, U., Warrington, J., Gray, C., Keck, W. & Mous, J. (1998). Bacterial transcript imaging by hybridization of total RNA to oligonucleotide arrays. Nature Biotechnol. 16, 45-48. [ abstract ]
DeRisi, J. L., Iyer, V. R. & Brown, P. O. (1997). Exploring the metabolic and genetic control of gene expression on a genomic scale. Science 278, 680-686. [ abstract ]
Dujon, B. (1998). European Functional Analysis Network (EUROFAN) and the functional analysis of the Saccharomyces cerevisiae genome. Electrophoresis 19, 617-624. [ abstract ]
Durrieu, G., Letellier, T., Antoch, J., Deshouillers, J. M., Malgat, M. & Mazat, J. P. (1997). Identification of mitochondrial deficiency using principal component analysis. Mol. Cell. Biochem. 174, 149-156. [ abstract ]
Ehlde, M. & Zacchi, G. (1996). Influence of experimental errors on the determination of flux control coefficients from transient metabolic concentrations. Biochem. J. 313, 721-727. [ abstract ]
Eisen, M. B., Spellman, P. T., Brown, P. O. & Botstein, D. (1998). Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 95, 14863-14868. [ abstract ]
Fell, D. A. (1992). Metabolic Control Analysis - a survey of its theoretical and experimental development. Biochem. J. 286, 313-330.
Fell, D. A. (1996). Understanding the Control of Metabolism. Portland Press, London. [ synopsis ]
Fell, D. A. (1998). Increasing the flux in metabolic pathways: A metabolic control analysis perspective. Biotechnol. Bioeng. 58, 121-124.
Fell, D. A. & Sauro, H. M. (1985). Metabolic control and its analysis. Additional relationships between elasticities and control coefficients. Eur. J. Biochem. 148, 555-561. [ abstract ]
Fell, D. A. & Thomas, S. (1995). Physiological control of metabolic flux: the requirement for multisite modulation. Biochem. J. 311, 35-39. [ abstract ]
Forterre, P. (1997a). Archaea: what can we learn from their sequences? Curr. Op. Genet. & Develop. 7, 764-770. [ abstract ]
Forterre, P. (1997b). Protein versus rRNA: Problems in rooting the universal tree of life. ASM News 63, 89-95.
Fuqua, C., Winans S.C. & Greenberg, E.P. (1996). Census and consensus in bacterial ecosystems: The LuxR-LuxI family of quorum-sensing transcriptional regulators. Annu. Rev. Microbiol. 50, 727-751. [ abstract ] [ full text ]
Gilbert, R. J., Goodacre, R., Woodward, A. M. & Kell, D. B. (1997). Genetic programming: A novel method for the quantitative analysis of pyrolysis mass spectral data. Anal. Chem. 69, 4381-4389. [ abstract (requires subscription) ]
Goffeau, A., Barrell, B. G., Bussey, H., Davis, R. W., Dujon, B., Feldmann, H., Galibert, F., Hoheisel, J. D., Jacq, C., Johnston, M., Louis, E. J., Mewes, H. W., Murakami, Y., Philippsen, P., Tettelin, H. & Oliver, S. G. (1996). Life With 6000 Genes. Science 274, 546-567. [ abstract ]
Goodacre, R. & Kell, D. B. (1996). Pyrolysis mass spectrometry and its applications in biotechnology. Curr. Opinion Biotechnol. 7, 20-28. [ abstract ] [ full text ]
Goodacre, R., Kell, D. B. & Bianchi, G. (1993). Rapid assessment of the adulteration of virgin olive oils by other seed oils using pyrolysis mass spectrometry and artificial neural networks. J. Sci. Food Agri. 63, 297-307. [ abstract ] [ condensed paper ]
Goodacre, R., Neal, M. J. & Kell, D. B. (1994a). Rapid and quantitative analysis of the pyrolysis mass spectra of complex binary and tertiary mixtures using multivariate calibration and artificial neural networks. Anal. Chem. 66, 1070-1085. [ abstract ]
Goodacre, R., Neal, M. J. & Kell, D. B. (1996a). Quantitative analysis of multivariate data using artificial neural networks: a tutorial review and applications to the deconvolution of pyrolysis mass spectra. Zentralblatt. für Bakteriologie 284, 516-539. [ abstract ] [ full paper ]
Goodacre, R., Rooney, P. J. & Kell, D. B. (1998a). Rapid analysis of microbial systems using vibrational spectroscopy and supervised learning methods: application to the discrimination between methicillin-resistant and methicillin-susceptible Staphylococcus aureus. In Proc. SPIE (Infrared Spectroscopy: New Tool in Medicine), vol. 3257 (ed. M. Jackson and H. H. Mantsch), pp. 220-229. SPIE, San Jose, California, USA.
Goodacre, R., Timmins, É. M., Burton, R., Kaderbhai, N., Woodward, A., Kell, D. B. & Rooney, P. J. (1998b). Rapid identification of urinary tract infection bacteria using hyperspectral, whole organism fingerprinting and artificial neural networks. Microbiol. 144, 1157-1170. [ abstract ]
Goodacre, R., Timmins, É. M., Rooney, P. J., Rowland, J. J. & Kell, D. B. (1996b). Rapid identification of Streptococcus and Enterococcus species using diffuse reflectance-absorbance Fourier transform infrared spectroscopy and artificial neural networks. FEMS Microbiol. Lett. 140, 233-239. [ abstract ] [ full text ]
Goodacre, R., Trew, S., Wrigley-Jones, C., Neal, M. J., Maddock, J., Ottley, T. W., Porter, N. & Kell, D. B. (1994b). Rapid screening for metabolite overproduction in fermentor broths, using pyrolysis mass spectrometry with multivariate calibration and artificial neural networks. Biotechnol. Bioeng. 44, 1205-1216. [ full paper ]
Heinrich, R. & Rapoport, T. A. (1973). Linear theory of enzymatic chains: its application for the analysis of the crossover theorem and of the glycolysis of human erythrocytes. Acta Biol. Med. Germ. 31, 479-94.
Heinrich, R. & Rapoport, T. A. (1974). A linear steady-state treatment of enzymatic chains. General properties, control and effector strength. Eur. J. Biochem. 42, 89-95.
Heinrich, R. & Schuster, S. (1996). The Regulation of Cellular Systems. Chapman & Hall, New York. [ synopsis ]
Herweijer, M. A., Berden, J. A. & Slater, E. C. (1986). Uncoupler-inhibitor titrations of ATP-driven reverse electron-transfer in bovine submitochondrial particles provide evidence for direct interaction between ATPase and NADH-Q oxidoreductase. Biochim. Biophys. Acta 849, 276-287. [ abstract ]
Hieter, P. & Boguski, N. (1997). Functional genomics: it's all how you read it. Science 278, 601-602.
Hinton, J. C. D. (1997). The Escherichia coli genome sequence: the end of an era or the start of the FUN? Mol. Microbiol. 26, 417-422.
Hitchens, G. D. & Kell, D. B. (1983a). On the functional unit of energy coupling in photophosphorylation by bacterial chromatophores. Biochim. Biophys. Acta 723, 308-316.
Hitchens, G. D. & Kell, D. B. (1983b). Uncouplers can shuttle rapidly between localised energy coupling sites during photophosphorylation by chromatophores of Rhodopseudomonas capsulata N22. Biochem. J. 212, 25-30. [ abstract ]
Ho, M. W. (1998). The Rainbow and the Worm: the Physics of Organisms, Second edition. World Scientific, Singapore. [ synopsis ]
Hofmeyr, J.-H. S., Kacser, H. & van der Merwe, K. J. (1986). Metabolic control analysis of moiety-conserved cycles. Eur. J. Biochem. 155, 631-641. [ abstract ]
Holms, H. (1996). Flux analysis and control of the central metabolic pathways in Escherichia coli. FEMS Microbiol. Rev. 19, 85-116. [ abstract ]
Holms, W. H., Hamilton, I. D. & Mousdale, D. (1991). Improvements to microbial productivity by analysis of metabolic fluxes. J. Chem. Technol. Biotechnol. 50, 139-141.
Kacser, H. (1983). The control of enzyme systems in vivo: elasticity analysis of the steady state. Biochem. Soc. Trans. 11, 35-40.
Kacser, H. & Acerenza, L. (1993). A universal method for achieving increases in metabolite production. Eur. J. Biochem. 216, 361-367. [ abstract ]
Kacser, H. & Burns, J. A. (1973). The control of flux. In Rate Control of Biological Processes. Symposium of the Society for Experimental Biology Vol 27 (ed. D. D. Davies), pp. 65-104. Cambridge University Press, Cambridge.
Kaprelyants, A. S. & Kell, D. B. (1992). Rapid assessment of bacterial viability and vitality using rhodamine 123 and flow cytometry. J. Appl. Bacteriol. 72, 410-422.
Kaprelyants, A. S. & Kell, D. B. (1993). Dormancy in stationary-phase cultures of Micrococcus luteus: flow cytometric analysis of starvation and resuscitation. Appl. Environ. Microbiol. 59, 3187-3196.
Kaprelyants, A. S., Mukamolova, G. V. & Kell, D. B. (1994). Estimation of dormant Micrococcus luteus cells by penicillin lysis and by resuscitation in cell-free spent medium at high dilution. FEMS Microbiol. Lett. 115, 347-352.
Kaprelyants, A. S., Mukamolova, G. V., Kormer, S. S., Weichart, D. H., Young, M. & Kell, D. B. (1999). Intercellular signalling and the multiplication of prokaryotes: bacterial cytokines. Symp. Soc. Gen. Microbiol. in the press. [ meeting announcement ]
Kell, D. B. (1979). On the functional proton current pathway of electron transport phosphorylation: an electrodic view. Biochim. Biophys. Acta 549, 55-99.
Kell, D. B. (1987). Forces, fluxes and the control of microbial growth and metabolism. The twelfth Fleming lecture. J. Gen. Microbiol. 133, 1651-1665.
Kell, D. B. (1988). Protonmotive energy-transducing systems: some physical principles and experimental approaches. In Bacterial Energy Transduction (ed. C. J. Anthony), pp. 429-490. Academic Press, London.
Kell, D. B. (1992). The protonmotive force as an intermediate in electron transport-linked phosphorylation: problems and prospects. Curr. Top. Cell. Reg. 33, 279-289.
Kell, D. B. (1998). Fom code to mode for orphan genes. Trends Biotechnol. 16, 491-493.
Kell, D. B. & Hitchens, G. D. (1983). Coherent properties of the membranous systems of electron transport phosphorylation. In Coherent Excitations in Biological Systems (ed. H. Fröhlich and F. Kremer), pp. 178-198. Springer-Verlag, Berlin.
Kell, D. B., Kaprelyants, A. S. & Grafen, A. (1995). On pheromones, social behaviour and the functions of secondary metabolism in bacteria. Trends Ecol. Evol. 10, 126-129.
Kell, D. B., Kaprelyants, A. S., Weichart, D. H., Harwood, C. L. & Barer, M. R. (1998). Viability and activity in readily culturable bacteria: a review and discussion of the practical issues,. Antonie van Leeuwenhoek 73, 169-187. [ abstract ]
Kell, D. B., Ryder, H. M., Kaprelyants, A. S. & Westerhoff, H. V. (1991). Quantifying heterogeneity: Flow cytometry of bacterial cultures. Antonie van Leeuwenhoek 60, 145-158. [ abstract ]
Kell, D. B. & Sonnleitner, B. (1995). GMP - Good Modelling Practice: an essential component of good manufacturing practice. Trends Biotechnol. 13, 481-492.
Kell, D. B., van Dam, K. & Westerhoff, H. V. (1989). Control analysis of microbial growth and productivity. Symp. Soc. Gen. Microbiol. 44, 61-93.
Kell, D. B. & Welch, G. R. (1991). No turning back, Reductonism and Biological Complexity. Times Higher Educational Supplement 9th August, 15.
Kell, D. B. & Westerhoff, H. V. (1986a). Metabolic control theory: its role in microbiology and biotechnology. FEMS Microbiol. Rev. 39, 305-320.
Kell, D. B. & Westerhoff, H. V. (1986b). Towards a rational approach to the optimization of flux in microbial biotransformations. Trends Biotechnol. 4, 137-142.
Kell, D. B. & Westerhoff, H. V. (1990). Control analysis of organised multienzyme systems. In Structural and organizational aspects of metabolic regulation (ed. P. Srere, M. E. Jones and C. Mathews), pp. 273-289. Alan R. Liss, New York.
Kholodenko, B. N., Cascante, M., Hoek, J. B., Westerhoff, H. V. & Schwaber, J. (1998). Metabolic design: How to engineer a living cell to desired metabolite concentrations and fluxes. Biotechnol. Bioeng. 59, 239-247.
Koonin, E. V. & Galperin, M. Y. (1997a). Prokaryotic genomes: the emerging paradigm of genome-based microbiology. Curr. Op. Gen. & Develop. 7, 757-763. [ abstract ]
Koonin, E. V., Mushegian, A. R., Galperin, M. Y. & Walker, D. R. (1997b). Comparison of archaeal and bacterial genomes: computer analysis of protein sequences predicts novel functions and suggests a chimeric origin for the archaea. Mol. Microbiol. 25, 619-637. [ abstract ]
Langley, P., Simon, H. A., Bradshaw, G. L. & Zytkow, J. M. (1987). Scientific Discovery: Computational exploration of the creative processes. MIT Press, Cambridge, MA. [ MIT Press description ]
Letellier, T., Malgat, M., Rossignol, R. & Mazat, J. P. (1998). Metabolic control analysis and mitochondrial pathologies. Mol. Cell. Biochem. 184, 409-417. [ abstract ]
Lopez de Felipe, F., Kleerebezem, M., de Vos, W. M. & Hugenholtz, J. (1998). Cofactor engineering: a novel approach to metabolic engineering in Lactococcus lactis by controlled expression of NADH oxidase. J. Bacteriol. 180, 3804-3808. [ abstract ]
Mazat, J. P., Letellier, T., Bedes, F., Malgat, M., Korzeniewski, B., Jouaville, L. S. & Morkuniene, R. (1997). Metabolic control analysis and threshold effect in oxidative phosphorylation: Implications for mitochondrial pathologies. Mol. Cell. Biochem. 174, 143-148. [ abstract ]
Mazat, J. P., Letellier, T., Malgat, M., Rossignol, R., Korzeniewski, B., Demaugre, F. & Leroux, J. P. (1998). Inborn errors of metabolism in the light of metabolic control analysis. Biochem. Soc. Trans. 26, 141-145.
McVeigh, H. P., Munro, J. & Embley, T. M. (1996). Molecular evidence for the presence of novel actinomycete lineages in a temperate forest soil. J. Ind. Microbiol. 17, 197-204. [ abstract ]
Mendes, P. (1993). GEPASI: a software package for modelling the dynamics, steady states and control of biochemical and other systems. Comput. Appl. Biosci. 9, 563-571. [abstract]
Mendes, P. (1997). Biochemistry by numbers: simulation of biochemical pathways with Gepasi 3. Trends Biochem. Sci. 22, 361-363.
Mendes, P. & Kell, D. B. (1997). Making cells work: metabolic engineering for everyone. Trends Biotechnol. 15, 6-7.
Mendes, P. & Kell, D. B. (1998a). Non-linear optimization of biochemical pathways: applications to metabolic engineering and parameter estimation. Bioinformatics 14, 869-883. [ abstract ]
Mendes, P. & Kell, D. B. (1998b). Numerical optimisation and simulation for rational metabolic engineering. In Biothermokinetics in the post genomic era (ed. C. Larsson, I.-L. Pahlman and L. Gustaffson), pp. 345-349. Chalmers Repro Service, Göteborg.
Mendes, P., Kell, D. B. & Welch, G. R. (1995). Metabolic channeling in organized enzyme systems: experiments and models. In Enzymology in vivo (ed. K. M. Brindle), pp. 1-19. JAI Press, London.
Mendes, P., Kell, D. B. & Westerhoff, H. V. (1992). Channelling can decrease pool size. Eur. J. Biochem. 204, 257-266. [ abstract ]
Mendes, P., Kell, D. B. & Westerhoff, H. V. (1996). Why and when channeling can decrease pool size at constant net flux in a simple dynamic channel. Biochim. Biophys. Acta 1289, 175-186. [ abstract ]
Michie, D., Spiegelhalter, D. J. & Taylor, C. C. (1994). Machine learning: neural and statistical classification. In Ellis Horwood Series in Artificial Inteligence (ed. J. Campbell). Ellis Horwood, Chichester. [ full text ]
Mitchell, P. (1966). Chemiosmotic coupling in oxidative and photosynthetic phosphorylation. Biol. Rev. 41, 445-502.
Mukamolova, G. V., Kaprelyants, A. S., Young, D. I., Young, M. & Kell, D. B. (1998). A bacterial cytokine. Proc. Natl. Acad. Sci. USA 95, 8916-8921. [ abstract ]
Nicholls, D. G. & Ferguson, S. J. (1992). Bioenergetics 2. Academic Press, London. [ synopsis ]
Niederberger, P., Prasad, R., Miozzari, G. & Kacser, H. (1992). A Strategy for increasing an in vivo flux by genetic manipulations - the tryptophan system of yeast. Biochem. J. 287, 473-479. [abstract]
Oldroyd, D. (1986). The arch of knowledge: an introduction to the history of the philosophy and methodology of science. Methuen, New York.
Oliver, S. G. (1996). From DNA sequence to biological function. Nature 379, 597-600. [ abstract ]
Oliver, S. G. & Baganz, F. (1998). The yeast genome: systematic analysis of DNA sequence and biological function. In Genomics: commercial opportunities from a scientific revolution (ed. L. G. Copping, G. K. Dixon and D. J. Livingstone), pp. in press. Bios, Oxford.
Oliver, S. G., Winson, M. K., Kell, D. B. & Baganz, F. (1998). Systematic functional analysis of the yeast genome. Trends Biotechnol. 16, 373-378. [ abstract ]
Ovádi, J. (1995). Cell architecture and metabolic channeling. Springer-Verlag, New York. [ entry in Amazon.com ]
Raju, G. K. & Cooney, C. L. (1998). Active learning from process data. AIChE J. 44, 2199-2211.
Reder, C. (1988). Metabolic control theory: a structural approach. J. Theoret. Biol. 135, 175-201. [ abstract ]
Reich, J. G. & Sel'kov, E. E. (1981). Energy metabolism of the cell: a theoretical treatise. Academic Press, London.
Rich, E. & Knight, K. (1991). Artificial Intelligence. McGraw Hill, New York. [ synopsis ]
Rivera, M. C., Jain, R., Moore, J. E. & Lake, J. A. (1998). Genomic evidence for two functionally distinct gene classes. Proc. Natl. Acad. Sci. USA 95, 6239-6244. [ abstract ]
Schena, M., Shalon, D., Heller, R., Chai, A., Brown, P. O. & Davis, R. W. (1996). Parallel human genome analysis - microarray-based expression monitoring of 1000 genes. Proc. Natl. Acad. Sci. USA 93, 10614-10619. [ abstract ]
Schlosser, P. M., Holcomb, T. & Bailey, J. E. (1993). Determining metabolic sensitivity coefficients directly from experimental data. Biotechnol. Bioeng. 41, 1027-1038.
Schuster, R. & Holzhütter, H. G. (1995). Use of mathematical models for predicting the metabolic effect of large-scale enzyme-activity alterations: application to enzyme deficiencies of red blood cells. Eur. J. Biochem. 229, 403-418. [ abstract ]
Shaw, A. D., diCamillo, A., Vlahov, G., Jones, A., Bianchi, G., Rowland, J. & Kell, D. B. (1997). Discrimination of the variety and region of origin of extra virgin olive oils using C-13 NMR and multivariate calibration with variable reduction. Anal. Chim. Acta 348, 357-374.
Simpson, T. W., Colon, G. E. & Stephanopoulos, G. (1995). 2 Paradigms of metabolic engineering applied to amino acid biosynthesis. Biochem. Soc. Trans. 23, 381-387.
Simpson, T. W., Shimizu, H. & Stephanopoulos, G. (1998). Experimental determination of group flux control coefficients in metabolic networks. Biotechnol. Bioeng. 58, 149-153.
Small, J. R. (1993). Flux control coefficients determined by inhibitor titration: the design and analysis of experiments to minimize errors. Biochem. J. 296, 423-433. [ abstract ]
Small, J. R. & Kacser, H. (1993a). Responses of metabolic systems to large changes in enzyme activities and effectors .1. The linear treatment of unbranched chains. Eur. J. Biochem. 213, 613-624. [ abstract ]
Small, J. R. & Kacser, H. (1993b). Responses of metabolic systems to large changes in enzyme activities and effectors .2. The linear treatment of branched pathways and metabolite concentrations - assessment of the general nonlinear case. Eur. J. Biochem. 213, 625-640. [ abstract ]
Smith, V., Botstein, D. & Brown, P. O. (1995). Genetic footprinting - A genomic strategy for determining a gene's function given its sequence. Proc. Natl. Acad. Sci. USA 92, 6479-6483. [ abstract ]
Smith, V., Chou, K. N., Lashkari, D., Botstein, D. & Brown, P. O. (1996). Functional analysis of the genes of yeast chromosome V by genetic footprinting. Science 274, 2069-2074. [ abstract ]
Spellman, P. T., Sherlock, G., Zhang, M. Q., Iyer, V. R., Anders, K., Eisen, M. B., Brown, P. O., Botstein, D. & Futcher, B. (1998). Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol. Biol. Cell 9, 3273-3297. [ abstract ]
Stephanopoulos, G. & Simpson, T. W. (1997). Flux amplification in complex metabolic networks. Chem. Eng. Sci. 52, 2607-2627.
Taylor, J., Goodacre, R., Wade, W. G., Rowland, J. J. & Kell, D. B. (1998). The deconvolution of pyrolysis mass spectra using genetic programming: application to the identification of some Eubacterium species. FEMS Microbiol. Lett. 160, 237-246. [ abstract ]
Teusink, B., Baganz, F., Westerhoff, H. V. & Oliver, S. G. (1998). Metabolic Control Analysis as a tool in the elucidation of the function of novel genes. In Methods in Microbiology: Yeast gene analysis (ed. M. F. Tuite and A. J. P. Brown), pp. 297-336. Academic Press, London. [ book synopsis ]
Thatcher, J. W., Shaw, J. M. & Dickinson, W. J. (1998). Marginal fitness contributions of nonessential genes in yeast. Proc. Natl. Acad. Sci. USA 95, 253-257. [ abstract ]
Thomas, S. & Fell, D. A. (1995). Error and bias in control coefficients calculated from elasticities. Biochem. Soc. Trans. 23, S294.
Thomas, S. & Fell, D. A. (1998). The role of multiple enzyme activation in metabolic flux control. Adv. Enz. Reg. 38, 65-85.
Velculescu, V. E., Zhang, L., Zhou, W., Vogelstein, J., Basrai, M. A., Bassett, D. E., Hieter, P., Vogelstein, B. & Kinzler, K. W. (1997). Characterization of the yeast transcriptome. Cell 88, 243-251. [ abstract ]
Weiss, S. H. & Kulikowski , C. A. (1991). Computer systems that Learn: classification and prediction methods from statistics, neural networks, machine learning, and expert systems. Morgan Kaufmann Publishers, San Mateo, CA.
Welch, G. R. & Kell, D. B. (1986). Not just catalysts; the bioenergetics of molecular machines. In The Fluctuating Enzyme (ed. G. Welch, .R.), pp. 451-492. John Wiley, New York.
Westerhoff, H. V., Hellingwerf, K. J. & van Dam, K. (1983). Thermodynamic efficiency of microbial growth is low but optimal for maximal growth rate. Proc. Natl. Acad. Sci. USA 80, 305-309.
Westerhoff, H. V. & Kell, D. B. (1987). Matrix method for determining the steps most rate-limiting to metabolic fluxes in biotechnological processes. Biotechnol. Bioeng. 30, 101-107.
Westerhoff, H. V. & Kell, D. B. (1988). A control theoretical analysis of inhibitor titrations of metabolic channelling. Comments Mol. Cell. Biophys. 5, 57-107.
Westerhoff, H. V. & Kell, D. B. (1996). What BioTechnologists knew all along...? J. Theoret. Biol. 182, 411-420. [abstract]
Westerhoff, H. V. & van Dam, K. (1987). Thermodynamics and control of biological free energy transduction. Elsevier, Amsterdam.
Wilkins, M. R., Williams, K. L., Appel, R. D. & Hochstrasser, D. F. (1997). Proteome research: new frontiers in functional genomics. Springer, Berlin. [ synopsis ]
Williams, R. J. (1956). Biochemical Individuality. John Wiley, New York.
Winson, M. K., Goodacre, R., Timmins, É. M., Jones, A., Alsberg, B. K., Woodward, A. M., Rowland, J. J. & Kell, D. B. (1997). Diffuse reflectance absorbance spectroscopy taking in chemometrics (DRASTIC). A hyperspectral FT-IR-based approach to rapid screening for metabolite overproduction. Anal. Chim. Acta 348, 273-282. [ abstract ]
Winson, M. K., Todd, M., Rudd, B. A. M., Jones, A., Alsberg, B. K., Woodward, A. M., Goodacre, R., Rowland, J. J. & Kell, D. B. (1998). A DRASTIC (Diffuse Reflectance Absorbance Spectroscopy Taking in Chemometrics) approach for the rapid analysis of microbial fermentation products: quantification of aristeromycin and neplanocin A in Streptomyces citricolor broths. In New frontiers in screening for microbial biocatalysts (ed. K. Kieslich, C. P. van der Beek, J. A. M. de Bont and W. J. J. van den Tweel), pp. 185-191. Elsevier, Amsterdam.
Wodicka, L., Dong, H. L., Mittmann, M., Ho, M. H. & Lockhart, D. J. (1997). Genome-wide expression monitoring in Saccharomyces cerevisiae. Nature Biotechnol. 15, 1359-1367. [ abstract ]
[ index ]
Copyright © 1999 Douglas B. Kell and Pedro Mendes, All rights
reserved.
HTML composition by Pedro Mendes